Difference between revisions of "H-Allegro Gallery"
| Line 1: | Line 1: | ||
| + | |||
| + | == Direct simulation of propagating flames: 3D expanding or converging front == | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+ 3D expanding propane/air flame | ||
| + | |[[File:3DDNSEXPANDING0.jpg|450 px]] | ||
| + | |[[File:3DDNSEXPANDING1.jpg|450 px]] | ||
| + | |} | ||
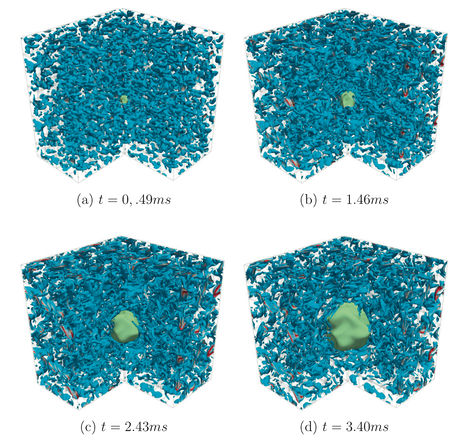
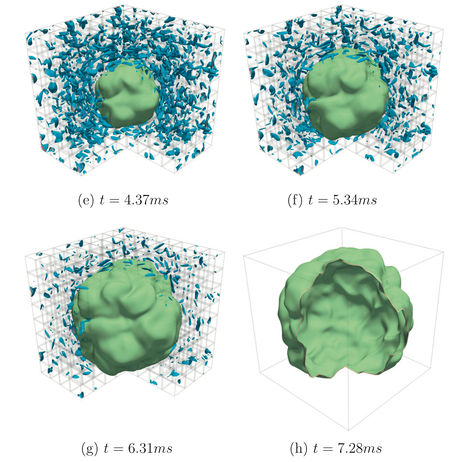
| + | Three dimensional simulation of a propane/air stoichiometric expanding flame. Iso-contours of vorticity (blue to red) and of reaction rate (green). Physical times range here from 0.49 to 7.28 ms. | ||
| + | *[[Media:albin.mpg| Dowload 3D expanding flame Movie (mpg file) ]] | ||
| + | |||
| + | |||
| + | *DNS of propane/air 3D expanding flame | ||
| + | *Mesh 480 x480 x 480 (~110 million grid points) ; dx~60 microns; 3x3x3 cubic cm | ||
| + | *Initial Passot-Pouquet spectrum then cold flow DNS for obtaining decreasing turbulence | ||
| + | * 512 proc, 70 000 CPU hours | ||
| + | * Comparison with EXPERIMENTAL & EEM (asymptotic modeling) approaches (cf. FLAMEX results) | ||
| + | |||
| + | | class="wikitable" | ||
| + | |+ 3D diverging and converging reacting fronts in turbulent flows | ||
| + | |[[File:3DDNSEXPANDING0.jpg|450 px]] | ||
| + | |[[File:3DDNSEXPANDING1.jpg|450 px]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | * E. Albin & Y. D’Angelo, Assessment of the Evolution Equation Modelling approach for three-dimensional expanding wrinkled premixed flames, Combustion & Flame, Vol. 159, Issue 5, pp 1932–1948, May 2012 http://dx.doi.org/10.1016/j.combustflame.2011.12.019 | ||
| + | |||
| + | |||
| + | |||
| + | == Direct simulation of propagating flames: 3D expanding or converging front == | ||
| + | |||
| + | |||
| + | |||
== 3D NSCBC modeling for transverse and corner outflows == | == 3D NSCBC modeling for transverse and corner outflows == | ||
| Line 30: | Line 63: | ||
| + | == No-slip wall acoustic boundary condition treatment in the incompressible limit : the NSWIL strategy == | ||
| − | + | Accurate and stable no-slip wall boundary condition for com- pressible flows is still an open problem for general high-order finite difference solvers. | |
| − | + | A characteristic formulation for the numerical treatment of acoustically reflecting no-slip wall boundary condition is presented and numerically validated for some discriminating situations. | |
| − | + | As an extension of the 3DNSCBC popular approach, this NSWIL strategy relaxes smoothly towards a 3DNSCBC strategy for a slipping wall – the Euler equations natural wall boundary condition – when the viscosity goes to zero. | |
| − | + | Using our in-house 6th order FD solver, some comparative tests were performed. | |
| − | + | In particular, we computed a pressure wave train in a 2D periodic channel, leading to standing acoustic waves. Long time runs using NSWIL strategy and involving 2.5 10^5 temporal iterations and more than 2000 acoustic reflections at the walls show no numerical instability while popular NSCBC strategy turns out to be unstable after less than 100 reflections. In that case, global mass conservation was very precisely ensured using NSWIL (relative loss < 6.10^-5 after 2000 acoustic reflections) while NSCBC induced a global variation above 1% before code crashed. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Revision as of 18:07, 21 March 2016
Contents
- 1 Direct simulation of propagating flames: 3D expanding or converging front
- 2 Direct simulation of propagating flames: 3D expanding or converging front
- 3 3D NSCBC modeling for transverse and corner outflows
- 4 No-slip wall acoustic boundary condition treatment in the incompressible limit : the NSWIL strategy
Direct simulation of propagating flames: 3D expanding or converging front
|
|
Three dimensional simulation of a propane/air stoichiometric expanding flame. Iso-contours of vorticity (blue to red) and of reaction rate (green). Physical times range here from 0.49 to 7.28 ms.
- DNS of propane/air 3D expanding flame
- Mesh 480 x480 x 480 (~110 million grid points) ; dx~60 microns; 3x3x3 cubic cm
- Initial Passot-Pouquet spectrum then cold flow DNS for obtaining decreasing turbulence
- 512 proc, 70 000 CPU hours
- Comparison with EXPERIMENTAL & EEM (asymptotic modeling) approaches (cf. FLAMEX results)
| class="wikitable"
|+ 3D diverging and converging reacting fronts in turbulent flows
| |
| |}
|}
- E. Albin & Y. D’Angelo, Assessment of the Evolution Equation Modelling approach for three-dimensional expanding wrinkled premixed flames, Combustion & Flame, Vol. 159, Issue 5, pp 1932–1948, May 2012 http://dx.doi.org/10.1016/j.combustflame.2011.12.019
Direct simulation of propagating flames: 3D expanding or converging front
3D NSCBC modeling for transverse and corner outflows
The limitations of usual three dimensional Navier–Stokes Characteristic Boundary Conditions (3D-NSCBC) for flows traveling in a direction that is oblique to the boundary may induce flow deformation at the vicinity of the outflow/ To limit errors generated at boundaries with flows having any arbitrary direction, we propose to organize the wave decomposition in a coordinate system that is attached to the local flow streamline crossing the boundary, because some modeled expressions are not frame independent. Compared to previous 3D-NSCBC, the modified strategy accounting for oblique waves is found to improve the outflow treatment for transverse outgoing vortices, up to vortices crossing an outflow corner. The method is also applied to an expanding laminar flame.

|
Outgoing vortex at upright corner. (a) density field (gray gradients) and Q-criterion iso-lines, 3D-NSCBC; (b) density field and Q-criterion iso-lines, 3D-NSCBC-TOM; (c) iso-U2, 3D-NSCBC; (d) iso-U2, 3D-NSCBC-TOM.

|

|
Left : Outgoing oblique vortex (a) Iso-U1, 3D-NSCBC; (b) iso-U1, 3D-NSCBC-TOM; (c) iso-U2, 3D-NSCBC; (d) iso-U2, 3D-NSCBC-TOM; (e) iso-Q criterion and density (gray gradients), 3D-NSCBC; (f) iso-Q criterion and density, 3D-NSCBC-TOM. Right : 2D expanding laminar premixed flame. (a, c, and e) 3D-NSCBC. (b, d, and f) 3D-NSCBC-TOM. (a and b) Temperature. (c and d) Density. (e and f) Reaction rates and velocity vectors.
- E. Albin, Y. D'Angelo & L. Vervisch, Flow streamline based Navier-Stokes Characteristic Boundary Conditions: modeling for transverse and corner outflows, Computers and Fluids, 51, 1, pp. 115-126, 2012 http://dx.doi.org/10.1016/j.compfluid.2011.08.005
- E. Albin, Y. D'Angelo & L. Vervisch, Using staggered grids with acoustic boundary conditions when solving compressible reactive Navier-Stokes equations, International Journal for Numerical Methods in Fluids, 2012 http://dx.doi.org/10.1002/fld.2520
No-slip wall acoustic boundary condition treatment in the incompressible limit : the NSWIL strategy
Accurate and stable no-slip wall boundary condition for com- pressible flows is still an open problem for general high-order finite difference solvers. A characteristic formulation for the numerical treatment of acoustically reflecting no-slip wall boundary condition is presented and numerically validated for some discriminating situations. As an extension of the 3DNSCBC popular approach, this NSWIL strategy relaxes smoothly towards a 3DNSCBC strategy for a slipping wall – the Euler equations natural wall boundary condition – when the viscosity goes to zero. Using our in-house 6th order FD solver, some comparative tests were performed. In particular, we computed a pressure wave train in a 2D periodic channel, leading to standing acoustic waves. Long time runs using NSWIL strategy and involving 2.5 10^5 temporal iterations and more than 2000 acoustic reflections at the walls show no numerical instability while popular NSCBC strategy turns out to be unstable after less than 100 reflections. In that case, global mass conservation was very precisely ensured using NSWIL (relative loss < 6.10^-5 after 2000 acoustic reflections) while NSCBC induced a global variation above 1% before code crashed.