H-Allegro Gallery

Direct simulation of propagating flames: 3D expanding or converging front

3D expanding propane/air flame

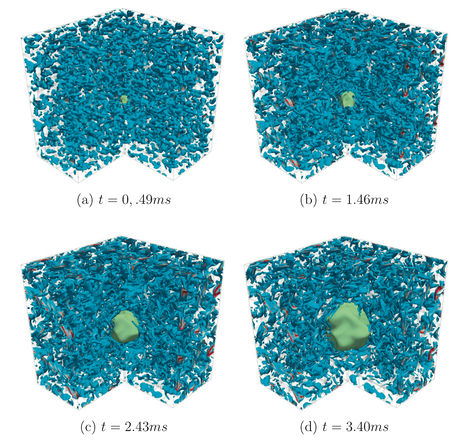
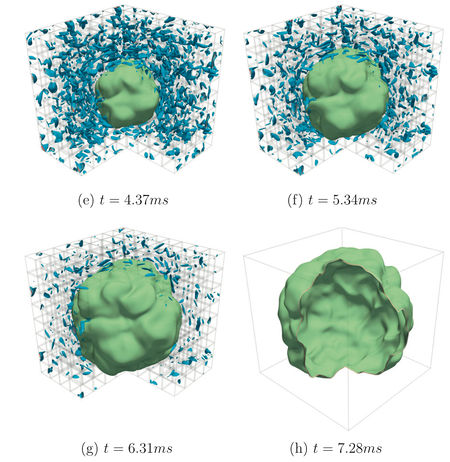
Three dimensional simulation of a propane/air stoichiometric expanding flame. Iso-contours of vorticity (blue to red) and of reaction rate (green). Physical times range here from 0.49 to 7.28 ms.

• Dowload 3D expanding flame Movie (mpg file)

3D expanding flame Movie (

• DNS of propane/air 3D expanding flame
• Mesh 480 x480 x 480 (~110 million grid points) ; dx~60 microns; 3x3x3 cubic cm
• Initial Passot-Pouquet spectrum then cold flow DNS for obtaining decreasing turbulence
• 512 proc, 70 000 CPU hours
• Comparison with EXPERIMENTAL & EEM (asymptotic modeling) approaches (cf. FLAMEX results)

• More details in E. Albin & Y. D’Angelo, Assessment of the Evolution Equation Modelling approach for three-dimensional expanding wrinkled premixed flames, Combustion & Flame, Vol. 159, Issue 5, pp 1932–1948, May 2012 http://dx.doi.org/10.1016/j.combustflame.2011.12.019

Direct simulation of propagating flames: 3D expanding or converging front

3D diverging and converging reacting fronts in turbulent flows, flame velocities

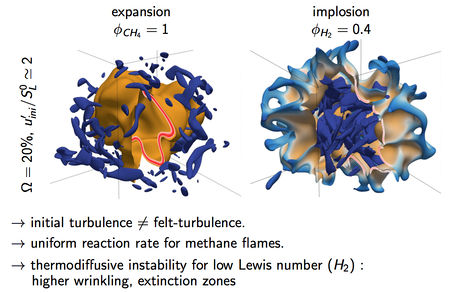
We are interested in DNS of converging and diverging reactive fronts in turbulent mixtures, for wet combustion analysis.

Four different mixtures are used : CH4/air φCH4 = 1 CH4/air/steam φCH4 = 1 H2/air φH2 = 0.4 H2/air/steam φH2 = 0.4 Ω = 0.0 Ω = 0.2 Ω = 0.0 Ω = 0.2

• different flame configurations : 4 laminar expansions (1.5cm)^3 4 laminar implosions (1.5cm)^3 6 turbulent expansions (1.8cm)^3 6 turbulent implosions (1.5cm)^3

→ 20 simulations. → between 512 and 4096 processes → 2.5 million cpu hours, ≃ 10Tb of analysed data.

3D NSCBC modeling for transverse and corner outflows

The limitations of usual three dimensional Navier–Stokes Characteristic Boundary Conditions (3D-NSCBC) for flows traveling in a direction that is oblique to the boundary may induce flow deformation at the vicinity of the outflow/ To limit errors generated at boundaries with flows having any arbitrary direction, we propose to organize the wave decomposition in a coordinate system that is attached to the local flow streamline crossing the boundary, because some modeled expressions are not frame independent. Compared to previous 3D-NSCBC, the modified strategy accounting for oblique waves is found to improve the outflow treatment for transverse outgoing vortices, up to vortices crossing an outflow corner. The method is also applied to an expanding laminar flame.

TOM strategy compared to 3D-NSCBC & NSCBC

Outgoing vortex at upright corner. (a) density field (gray gradients) and Q-criterion iso-lines, 3D-NSCBC; (b) density field and Q-criterion iso-lines, 3D-NSCBC-TOM; (c) iso-U2, 3D-NSCBC; (d) iso-U2, 3D-NSCBC-TOM.

TOM strategy compared to 3D-NSCBC & NSCBC

Left : Outgoing oblique vortex (a) Iso-U1, 3D-NSCBC; (b) iso-U1, 3D-NSCBC-TOM; (c) iso-U2, 3D-NSCBC; (d) iso-U2, 3D-NSCBC-TOM; (e) iso-Q criterion and density (gray gradients), 3D-NSCBC; (f) iso-Q criterion and density, 3D-NSCBC-TOM. Right : 2D expanding laminar premixed flame. (a, c, and e) 3D-NSCBC. (b, d, and f) 3D-NSCBC-TOM. (a and b) Temperature. (c and d) Density. (e and f) Reaction rates and velocity vectors.

More details on

• E. Albin, Y. D'Angelo & L. Vervisch, Flow streamline based Navier-Stokes Characteristic Boundary Conditions: modeling for transverse and corner outflows, Computers and Fluids, 51, 1, pp. 115-126, 2012 http://dx.doi.org/10.1016/j.compfluid.2011.08.005

• E. Albin, Y. D'Angelo & L. Vervisch, Using staggered grids with acoustic boundary conditions when solving compressible reactive Navier-Stokes equations, International Journal for Numerical Methods in Fluids, 2012 http://dx.doi.org/10.1002/fld.2520

No-slip wall acoustic boundary condition treatment in the incompressible limit : the NSWIL strategy

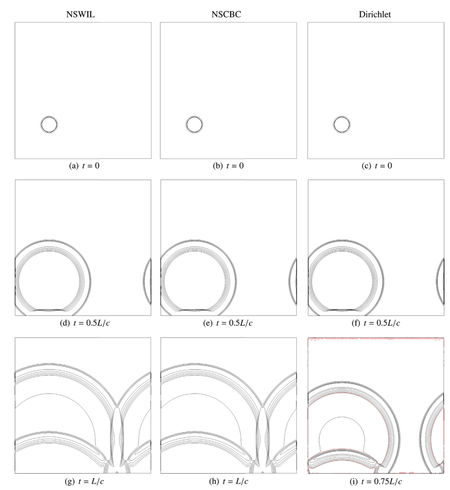
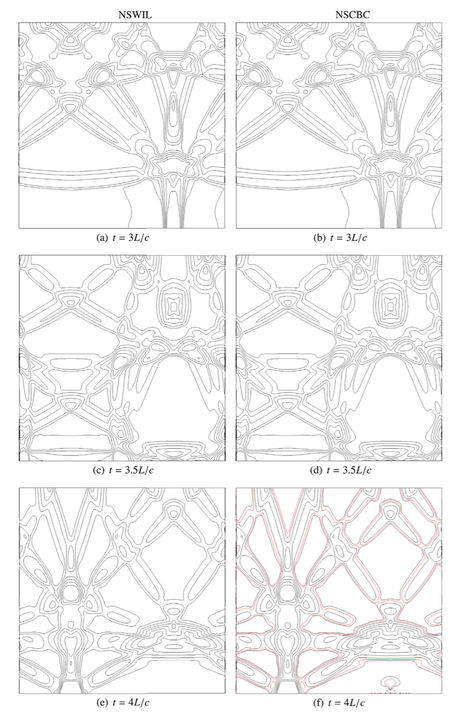
Accurate and stable no-slip wall boundary condition for compressible flows is still an open problem for general high-order finite difference solvers. A characteristic formulation for the numerical treatment of acoustically reflecting no-slip wall boundary condition is presented and numerically validated for some discriminating situations. As an extension of the 3DNSCBC popular approach, this NSWIL strategy relaxes smoothly towards a 3DNSCBC strategy for a slipping wall – the Euler equations natural wall boundary condition – when the viscosity goes to zero. Using our in-house 6th order FD solver, some comparative tests were performed. In particular, we computed a pressure wave train in a 2D periodic channel, leading to standing acoustic waves. Long time runs using NSWIL strategy and involving 2.5 􏰈 10^5 temporal iterations and more than 2000 acoustic reflections at the walls show no numerical instability while popular NSCBC strategy turns out to be unstable after less than 100 reflections. In that case, global mass conservation was very precisely ensured using NSWIL (relative loss < 6.10^-5 after 2000 acoustic reflections) while NSCBC induced a global variation above 1% before code crashed.

TOM strategy compared to 3D-NSCBC & NSCBC

Left : Comparison of the pressure contours for the acoustic reflection in a 2D box, for respectively 3DNSCBC, NSWIL and Dirichlet BC treatment at the wall, at different acoustic times of the computation. Notice the oscillations close to the lower wall and also along the upper wall, for the Dirichlet approach. Right : Same computation at later acoustic times, for NSWIL and NSCBC strategies. Notice the oscillations close to the lower wall (figure (f), bottom right) for the NSCBC approach, at acoustic time t = 4L/c.

• More details on M. Sjostrand-Cuif, Y. D'Angelo & E. Albin, No-slip Wall Acoustic Boundary Condition treatment in the Incompressible Limit, Computers & Fluids, Volume 86, Pages 92–102, November 2013. http://dx.doi.org/10.1016/j.compfluid.2013.07.015